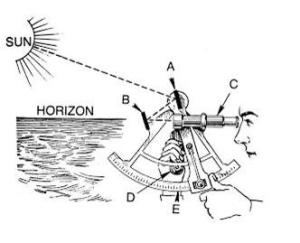
Aplikasi Trigonometri dalam Kehidupan Sehari-hari
Dalam kehidupan sehari – hari kita sering melihat seorang sedang mengukur jalan yang akan diperbaiki ataupun gedung bertingkat yang sedang dibangun. Para arsitek tersebut bekerja dengan menggunakan perbandingan trigonometri.
Trigonometri menemukan penggunaannya yang sempurna pada Arsitektur modern. Kurva-kurva nan indah pada permukaan baja, bebatuan, kayu, dan lain-lain dapat diwujudkan karena potensi yang besar dari ilmu ini.
Trigonometri menemukan penggunaannya yang sempurna pada Arsitektur modern. Kurva-kurva nan indah pada permukaan baja, bebatuan, kayu, dan lain-lain dapat diwujudkan karena potensi yang besar dari ilmu ini.
Teknologi pencitraan dari komputer dapat digunakan dalam dunia kedokteran secara luar biasa untuk menemukan sumber beberapa penyakit ganas.
Itu baru sebagian kecil dari manfaat trigonometri, perlu alasan lain untuk menemukan rumus-rumus trigonometri membantu hidup kita.
Berikut beberapa contoh penggunaan trigonometri dalam kehidupan sehari-hari, misalya dalam navigasi untuk menemukan jarak dari pantai ke suatu titik di laut.
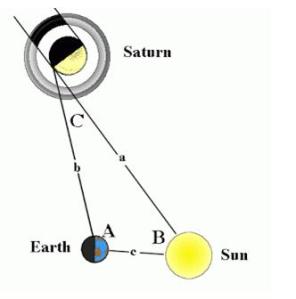 Fungsi sinus dan cosinus merupakan dasar bagi teori fungsi periodik seperti pada gelombang suara dan cahaya.
Fungsi sinus dan cosinus merupakan dasar bagi teori fungsi periodik seperti pada gelombang suara dan cahaya. Arsitek menggunakan trigonometri untuk menghitung beban struktural, kemiringan atap, permukaan tanah dan banyak aspek lain, termasuk bayangan matahari dan sudut cahaya
Arsitek menggunakan trigonometri untuk menghitung beban struktural, kemiringan atap, permukaan tanah dan banyak aspek lain, termasuk bayangan matahari dan sudut cahaya
sumber: rbyans di http://rbaryans.wordpress.com/2013/01/29/aplikasi-trigonometri-dalam-kehidupan-nyata/
Penerapan Rumus Trigonometri Dalam Kehidupan Sehari-hari
2. Tentukan nilai cos b dan cosec b, jika diketahui tan b = √2 !
Jawab :
B. Contoh Soal Sudut Istimewa Trigonometri
1. Tentukan nilai dari Sin 30° + Cos 45° !
2. Tentukan nilai dari Sin 45° . Tan 60° + Cos 45° . Cot 60° !
Jawab :
Contoh Soal:

a) dari data sin dan cos yang telah diperoleh didapatkan

b) dari data sin dan cos yang telah diperoleh didapatkan

Soal No. 4
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 3/5 dan sin B = 12/13. Sudut A dan sudut B adalah sudut lancip. Tentukan nilai dari cos (A + B)
Pembahasan
Cek nilai sin dan cos dengan segitiga seperti sebelumnya


Soal No. 5
Diketahui Δ PQR dengan ∠ P dan ∠ Q lancip. Jika tan P = 3/4 dan tan Q = 1/3, tentukan nilai dari cos R
Pembahasan
Cek sin cos kedua sudut P dan Q

sin P = 3/5, cos P = 4/5
Elzahra Oktameri
XI Mia 1
Penerapan Rumus Trigonometri Dalam Kehidupan Sehari-hari
Permasalahan 1 :
Triangulasi adalah metode navigasi yang menggunakan rumus trigonometri sebuah segitiga dalam mengkunci posisi dan lokasi objek. Logikanya seperti menggunakan kompas sebagai salah satu sudut segitiga dan 2 sudut lagi sebagai 2 posisi dengan jarak pemisah antara keduanya telah diketahui sebelumnya. Contoh : teknologi tringulasi satelit adalah GPS (Global Positioning System) yang memanfaatkan minimal 24 buah satelit yang mengorbitkan mengelilingi bumi dalam menentukan lokasi pengguna. Tringulasi satelit memungkinkan pengumpulan gambar grafis suatu wilayah secara remote. Tringulasi satelit ini akan menghasilkan foto dengan potensi error lebih kecil. Teknologi foto satelit ini bisa dimanfaatkan dalam melacak hotspot kebakaran hutan kalimantan,mengikuti perjalanan badai atau tornado gustav,dan juga operasi militer seperti misi intelejen inflitrasi pasukan ke Hotzone. Teknik triangulasi juga digunakan dalam astromi untuk menghitung jarak ke bintang-bintang terdekat.
Permasalahan ke-2:
Untuk menentukan waktu sholat,dalam Al-Qur'an Allah Swt berfirman : "Dirikianlah shalat sesungguhnya shalat itu kewajiban bagi orang mukmin yang ditentukan waktunya." Pembahasan masalah ini ditujukan untuk mengetahui peranan trigonometri (matematika) pada rumusan astronomis (dalam menentukan waktu shalat) di permukaaan bumi secara umum. Selain itu juga ingin ditunjukan bagaimana rumusan yang telah ada tersebut diterapkan,juga bagaimana sebenarnya islam mengatur tata cara beribadah utamanya dalam penentuan waktu shalat. Dengan menggunakan metode observasi data untuk deklinasi,equation of time maka diperoleh data dengan rumus {(t-d+w)/15 + (12?e) + I. Diketahui pula bahwa garis lintang dan garis bujur suatu tempat dipermukaan bumi adalah berbeda dan ini jelas berpengaruh pada waktu shalat. Akan diperoleh wakti shalat,dengan t diperolrh dengan rumus. Untuk menghitung waktu shalat tetap dilakukan sesuai dengan ketentuan yg telah ditetapkan. 30 Cos t = - tan 2x tan d,dan h untuk waktu ashar = Cot h = tan |-d|+1, waktu maghrib -1,waktu isya' -18,wakti shubuh -20,waktu zuhur tidak diperlukan karena 0, waktu syuruq -1 dan waktu dhuha 4.
sumber : (http://matematikasmkpcwn.blogspot.com/2013/09/aplikasi-trigonometri-pada-bidang.html)
A. Contoh Soal Konsep Trigonometri
1. Tentukan nilai sin a dan cot a, jika diketahui cos a = 3/5 !2. Tentukan nilai cos b dan cosec b, jika diketahui tan b = √2 !
Jawab :
Related
B. Contoh Soal Sudut Istimewa Trigonometri
1. Tentukan nilai dari Sin 30° + Cos 45° !
2. Tentukan nilai dari Sin 45° . Tan 60° + Cos 45° . Cot 60° !
Jawab :
Contoh Soal:
Soal No. 1
Dengan menggunakan rumus penjumlahan dua sudut tentukan nilai dari:
a) sin 75°
b) cos 75°
c) tan 105°
Dengan menggunakan rumus penjumlahan dua sudut tentukan nilai dari:
a) sin 75°
b) cos 75°
c) tan 105°
Pembahasan
a) Rumus jumlah dua sudut untuk sinus
a) Rumus jumlah dua sudut untuk sinus
| sin (A + B) = sin A cos B + cos A sin B |
sin 75° = sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4 (√6 + √2)
b) Rumus jumlah dua sudut untuk cosinus
= sin 45° cos 30° + cos 45° sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4 (√6 + √2)
b) Rumus jumlah dua sudut untuk cosinus
| cos (a + B) = cos A cos B − sin A sin B |
cos 75° = cos (45° + 30°)
= cos 45° ⋅ cos 30° − sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4 (√6 − √2)
c) Rumus jumlah dua sudut untuk tan
= cos 45° ⋅ cos 30° − sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4 (√6 − √2)
c) Rumus jumlah dua sudut untuk tan
 |
tan 105° = tan (60° + 45°)

Soal No. 2
Dengan menggunakan rumus selisih dua sudut tentukan nilai dari:
a) sin 15°
b) cos 15°
c) tan (3x − 2y)
Pembahasan
a) Rumus selisih dua sudut untuk sinus

Soal No. 2
Dengan menggunakan rumus selisih dua sudut tentukan nilai dari:
a) sin 15°
b) cos 15°
c) tan (3x − 2y)
Pembahasan
a) Rumus selisih dua sudut untuk sinus
| sin (A − B) = sin A cos B − cos A sin B |
sin 15° = sin 45° − 30°)
= sin 45° ⋅ cos 30° − cos 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4(√6 − √2)
b) Rumus selisih dua sudut untuk cosinus
= sin 45° ⋅ cos 30° − cos 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4(√6 − √2)
b) Rumus selisih dua sudut untuk cosinus
| cos (A − B) = cos A cos B + sin A sin B |
cos 15° = cos (45° − 30°)
= cos 45° ⋅ cos 30° + sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4(√6 + √2)
= cos 45° ⋅ cos 30° + sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4(√6 + √2)
c) Rumus selisih sudut untuk tan
 |
Sehingga


Soal No. 3
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 4/5 dan sin B = 12/13. Sudut A adalah sudut tumpul sedangkan sudut B adalah sudut lancip. Tentukan:
A. sin (A + B)
B. sin (A − B)
Pembahasan
Gambar segitiga untuk cek nilai sin dan cos kedua sudut, tentunya setelah itu aplikasikan rumus phytagoras untuk mendapatkan panjang sisi-sisi segitiga, seperti gambar berikut:

Nilai sin dan cos "sementara" untuk masing-masing sudut terlihat dari segitiga di atas. Dibilang sementara karena setelah itu kita harus tentukan positif atau negatifnya. Setelah dicocokkan dengan kuadrannya barulah didapat nilai sin atau cos yang benar.
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 4/5 dan sin B = 12/13. Sudut A adalah sudut tumpul sedangkan sudut B adalah sudut lancip. Tentukan:
A. sin (A + B)
B. sin (A − B)
Pembahasan
Gambar segitiga untuk cek nilai sin dan cos kedua sudut, tentunya setelah itu aplikasikan rumus phytagoras untuk mendapatkan panjang sisi-sisi segitiga, seperti gambar berikut:

Nilai sin dan cos "sementara" untuk masing-masing sudut terlihat dari segitiga di atas. Dibilang sementara karena setelah itu kita harus tentukan positif atau negatifnya. Setelah dicocokkan dengan kuadrannya barulah didapat nilai sin atau cos yang benar.
sin A = 4/5
cos A = 3/5
sin B =12/13
cos B = 5/13
cos A = 3/5
sin B =12/13
cos B = 5/13
Periksa ulang,
- Sudut A tumpul sehingga berada di kuadran II (antara 90 dan 180) . Lihat ilustrasi di bawah, untuk kuadran II nilai sin adalah positif, sehingga sin A benar 4/5. Sementara untuk cos A, karena dikuadran II, nilainya negatif, jadi cos A = − 3/5
- Sudut B lancip, sehingga berada di kuadran I (antara 0 dan 90). Baik nilai sin atau cos dikuadran 1 adalah positif, sehingga data di atas bisa langsung digunakan.

a) dari data sin dan cos yang telah diperoleh didapatkan

b) dari data sin dan cos yang telah diperoleh didapatkan

Soal No. 4
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 3/5 dan sin B = 12/13. Sudut A dan sudut B adalah sudut lancip. Tentukan nilai dari cos (A + B)
Pembahasan
Cek nilai sin dan cos dengan segitiga seperti sebelumnya

sin A = 3/5, cos A = 4/5
sin B = 12/13, cos B = 5/13
Kedua sudut adalah lancip hingga baik sin ataupun cos adalah positif semua.
Dari data yang telah diperoleh masukkan rumus untuk cos jumlah sudut

Soal No. 5
Diketahui Δ PQR dengan ∠ P dan ∠ Q lancip. Jika tan P = 3/4 dan tan Q = 1/3, tentukan nilai dari cos R
Pembahasan
Cek sin cos kedua sudut P dan Q

sin P = 3/5, cos P = 4/5
sin Q = 1/√10, cos Q = 3/√10
P + Q + R = 180 atau R = 180 - (P + Q)
cos R = cos (180 - (P + Q))
ingat cos (180 - x) = - cos x

Soal No. 6
Jika tan α = 1, tan β = 1/3 dengan α dan β sudut lancip maka sin (α − β) =....
A. 2/3 √5
B. 1/5 √5
C. 1/2
D. 2/5
E. 1/5
(UN 2007-2008)
Pembahasan
tan α = 1, jika digambarkan dalam sebuah segitiga seperti berikut:

Dari gambar terlihat:
sin α = 1/ √2
cos α = 1/ √2
tan β = 1/3, jika digambarkan dalam sebuah segitiga akan diperoleh nilai sin dan cosnya:

Diperoleh
sin β = 1/√10
cos β = 3/√10
Kembali ke soal, diminta sin (α − β) =....
Dengan rumus selisih dua sudut:

Jadi sin (α − β) = 1/5 √5
Soal No. 7
Jika A + B = π/3 dan cos A cos B = 5/8, maka cos (A − B) =....
A. 1/4
B. 1/2
C. 3/4
D. 1
E. 5/4
un hal 102
Pembahasan
Dari rumus selisih dua sudut untuk cosinus:
cos (A + B) = cos A cos B − sin A sin B
Masukkan data soal
1/2 = 5/8 − sin A sin B
sin A sin B = 5/8 − 1/2 = 1/8
Diminta cos (A − B) =....
cos (A − B) = cos A cos B + sin A sin B
= 5/8 + 1/8 = 6/8 = 3/4
Soal No. 8
ABC adalah sebuah segitiga. Jika sin A = 3/5 dan cotan B = 7, maka ∠C = .....
A. 30°
B. 45°
C. 60°
D. 90°
E. 135°
Pembahasan
Dari data sin A = 3/5 dan cotan B = 7 (atau kalau dari tan nya, tan B = 1/7), diperoleh

sin A = 3/5
cos A = 4/5
sin B = 1/5√2
cos B = 7/5√2
Jumlah sudut dalam suatu segitiga adalah 180, jadi A + B + C = 180° atau bisa juga C = 180 − (A + B)
Kembali ke soal, diminta ∠C, kita cari sin C dulu:
sin C = sin [180 − (A + B)]
sin C = sin (A + B), ingat kembali ada rumus sin (180 − x) = sin x
sin C = sin A cos B + cos A sin B

ingat cos (180 - x) = - cos x

Soal No. 6
Jika tan α = 1, tan β = 1/3 dengan α dan β sudut lancip maka sin (α − β) =....
A. 2/3 √5
B. 1/5 √5
C. 1/2
D. 2/5
E. 1/5
(UN 2007-2008)
Pembahasan
tan α = 1, jika digambarkan dalam sebuah segitiga seperti berikut:

Dari gambar terlihat:
sin α = 1/ √2
cos α = 1/ √2
tan β = 1/3, jika digambarkan dalam sebuah segitiga akan diperoleh nilai sin dan cosnya:

Diperoleh
sin β = 1/√10
cos β = 3/√10
Kembali ke soal, diminta sin (α − β) =....
Dengan rumus selisih dua sudut:

Jadi sin (α − β) = 1/5 √5
Soal No. 7
Jika A + B = π/3 dan cos A cos B = 5/8, maka cos (A − B) =....
A. 1/4
B. 1/2
C. 3/4
D. 1
E. 5/4
un hal 102
Pembahasan
Dari rumus selisih dua sudut untuk cosinus:
cos (A + B) = cos A cos B − sin A sin B
Masukkan data soal
1/2 = 5/8 − sin A sin B
sin A sin B = 5/8 − 1/2 = 1/8
Diminta cos (A − B) =....
cos (A − B) = cos A cos B + sin A sin B
= 5/8 + 1/8 = 6/8 = 3/4
Soal No. 8
ABC adalah sebuah segitiga. Jika sin A = 3/5 dan cotan B = 7, maka ∠C = .....
A. 30°
B. 45°
C. 60°
D. 90°
E. 135°
Pembahasan
Dari data sin A = 3/5 dan cotan B = 7 (atau kalau dari tan nya, tan B = 1/7), diperoleh

sin A = 3/5
cos A = 4/5
sin B = 1/5√2
cos B = 7/5√2
Jumlah sudut dalam suatu segitiga adalah 180, jadi A + B + C = 180° atau bisa juga C = 180 − (A + B)
Kembali ke soal, diminta ∠C, kita cari sin C dulu:
sin C = sin [180 − (A + B)]
sin C = sin (A + B), ingat kembali ada rumus sin (180 − x) = sin x
sin C = sin A cos B + cos A sin B

Sudut yang nilai sin nya 1/2 √2 adalah 45°
Elzahra Oktameri
XI Mia 1